深度学习基础知识
几种“学习”间的关系
机器学习—最大的概念
<让机器通过学习的方式得到一个可以解决问题的模型>
学习方法:KNN(K近邻),k means(k均值解决聚类问题),SVM,深度学习
机器学习,隐式学习
神经网络:输入层,隐藏层,输出层
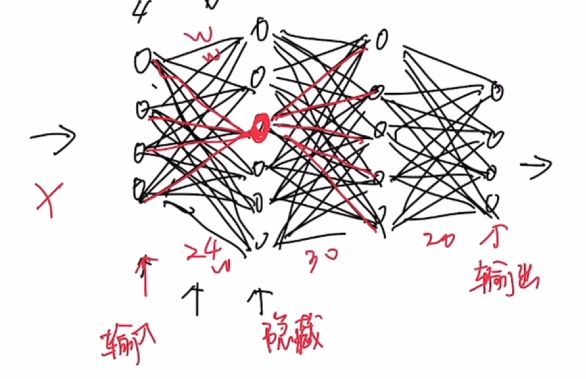
神经元
不改变网络层和算法的情况下,影响输出结果的是各神经元连接线路上的数值权重
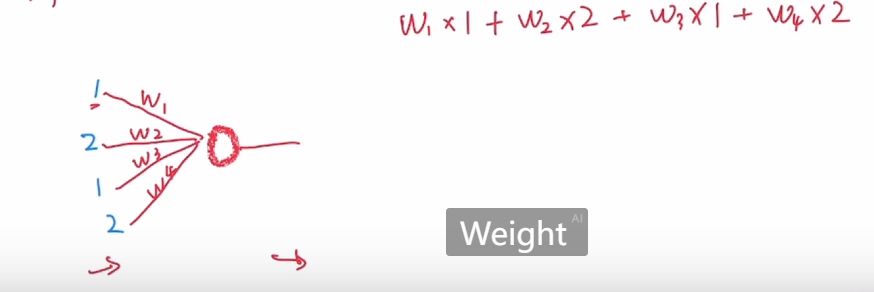
除了一系列加减乘除的线性变换外,还引入了激活函数
激活函数:阶跃函数(不用
希望通过梯度下降的方式求得参数更新的过程,阶跃函数无法正常求导,需要引入δ函数,因此使用别的函数作为激活函数Sigmoid,以此解决阶跃函数不可导的问题
Sigmoid:
$$ S(x)=\dfrac{1}{1+e^{-x}} $$
sigmoid导数: $$ S’(x)=\dfrac{e^{-x}}{(1+e^{-x})^2}=S(x)(1-S(x)) $$ Sigmoid函数及其导数的图像:
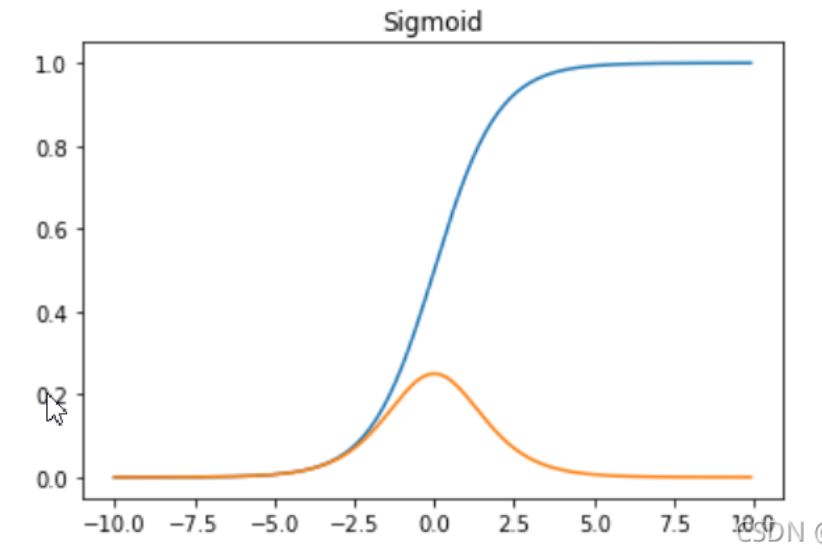
tanh:
$$ tanh=\dfrac{e^x-e^{-x}}{e^x+e^{-x}} $$
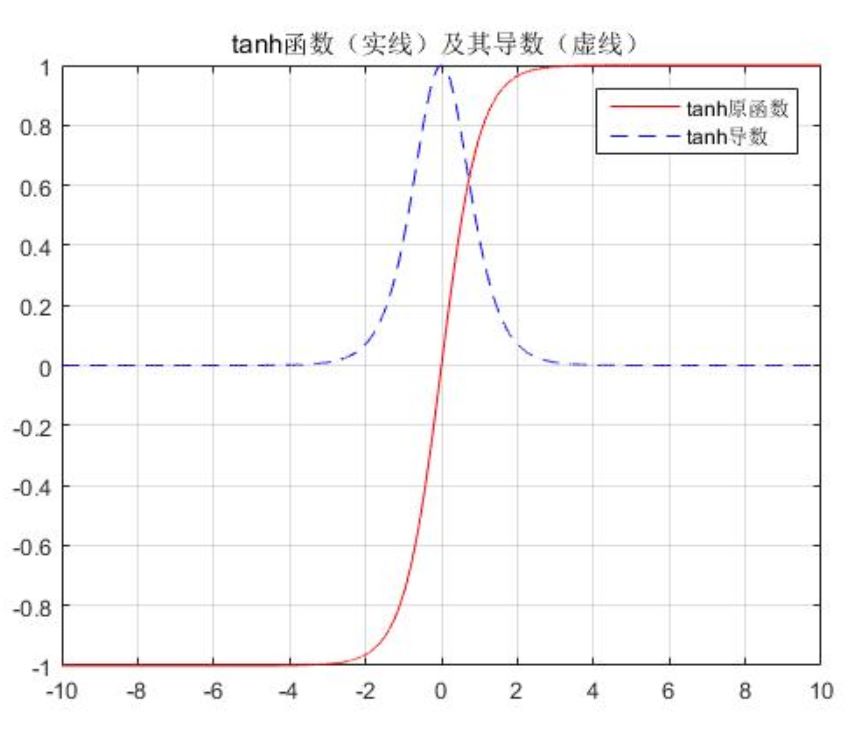
范围在(-1,1)间的激活函数
Relu函数
$$ f(x)=\begin{cases}x & x\geq0 \\0&x< 0\end{cases} $$
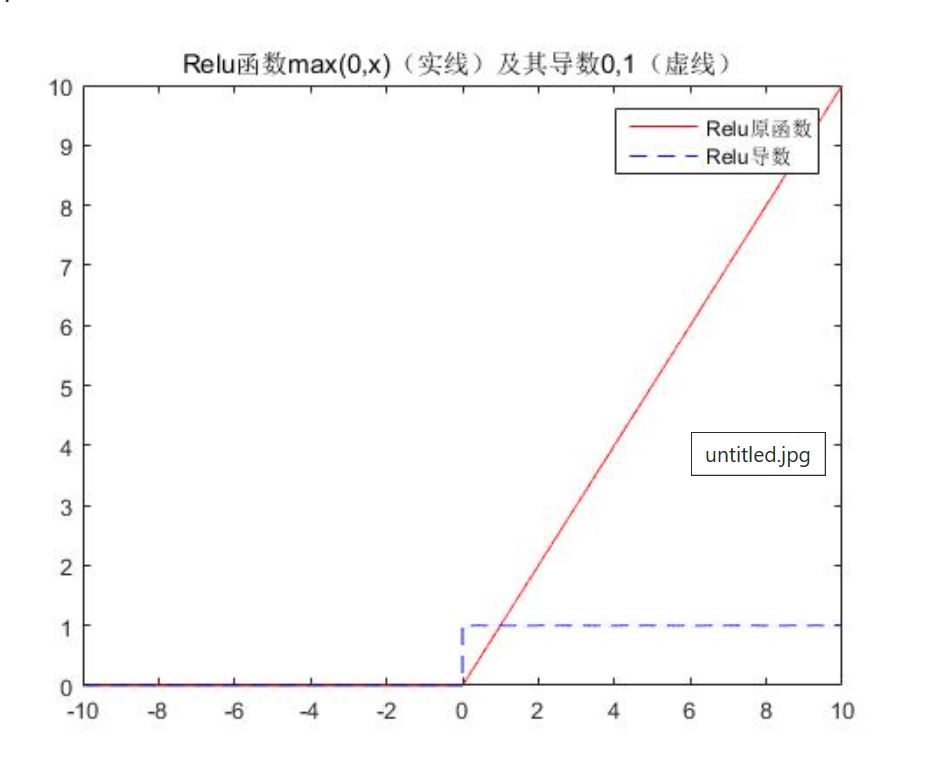
每个神经元所做的事: $$ g_{output}=g(w_1\times a+w_2\times b+w_3\times c+w_4\times d)—>relu $$ 注:a,b,c,d为权重值,神经元输出结果为各参数加权后通过一个relu函数所得的值
机器学习的目的是在给定前提情况下,寻找能得到最好输出的w参数们
梯度下降
如何寻找需要的W
通过当前所计算得出的结果与已知的正确结果做差,考虑到所得结果的正负号问题,采用对式子求平方的方式(平方好求导,绝对值不好求导) $$ L=(f(x)-y)^2 $$
L越小,模型性能越好,f(x)与参数w有关,因此L也是个关于w的函数。
可以通过调整w来使L的取值变小
动态更新W,eg:初始值w0,第一刻w1….. $$ W_1=W_0-lr\cdot \frac{\partial L}{\partial W_0} \\W_2=W_1-lr\cdot \frac{\partial L}{\partial W_1} \\… $$
局部最优/全局最优
类似高等数学函数章节中的极值和最值问题,局部导数为0的极值点不代表此处是整个函数的极值
ps:顺带吐槽一句,这个hugo对LateX数学公式的键入好像不是很友好,比如公式间的换行用要用\\,但是他识别代码的时候只识别一条杠\,这就导致像 $$ f(x)=\begin{cases}x & x\geq0 \\0&x< 0\end{cases} $$ 这种分段的函数会显示成这样 $$ f(x)=\begin{cases}x & x\geq0 \0&x< 0\end{cases} $$
byd后来我发现你只需要打3个\就能解决问题了。
