PyTorch基础笔记_01
常用库:torch,numpy,pandas,matplotlib
1
2
3
4
5
|
import torch
import numpy as np
import torch.nn as nn
from torch import optim as optim#优化器
import torch.nn.functional as F#用到的函数
|
基础使用
假设一个最简单的神经网络,没有隐藏层,只有输入层和输出层
eg:5个输入神经元,7个输出神经元,全连接
$$
y=w\cdot x+b
$$
x为输入层,形状为(1,5);
$$
\begin{bmatrix}x_1 & x_2&x_3&x_4&x_5\end{bmatrix}
$$
Y为输出层,形状为(1,7)#同上
$$
\begin{bmatrix}y_1 & y_2&y_3&y_4&y_5&y_6&y_7\end{bmatrix}
$$
w为权重,形状为(5,7) #全连接,
$$
\begin{bmatrix}w_{11}&w_{12}&w_{13}&w_{14}&w_{15}&w_{16}&w_{17}
\\w_{21} & w_{22}&w_{23}&w_{24}&w_{25}&w_{26}&w_{27}
\\w_{31} & w_{32}&w_{33}&w_{34}&w_{35}&w_{36}&w_{37}
\\w_{41} & w_{42}&w_{43}&w_{44}&w_{45}&w_{46}&w_{47}
\\w_{51} & w_{52}&w_{53}&w_{54}&w_{55}&w_{56}&w_{57}
\end{bmatrix}
$$
b为bias偏置,每个输出神经元输出前都会经过bias调整,所以形状为7
1
2
3
4
5
6
7
8
9
10
11
12
13
|
#定义各个参数
w=torch.randn(5,7,requires_grad=True)#生成5*7的随机数矩阵来填充w,同时设定w是需要后续进行梯度下降更新的属性,后半部分缺失会导致程序报错
b=torch.randn(7,requires_grad=True)
x=torch.randn(1,5)
Y=torch.randn(1,7)
lr=0.001#设置学习率
y=F.relu(x @ w + b) #x与w为矩阵,使用矩阵乘法@,同时调用事前导入为F的激活函数,这里选择relu函数(1)
#开始求loss,假定本案例为一个分类任务,选择交叉熵损失函数
loss=F.cross_entropy(y,Y)
#开始求参数梯度,进行梯度下降算法更新参数,pytorch提供了一个函数方法backward(),可以直接帮助我们找到所有参数梯度,无需自己算
loss.backward()#这步只求了梯度,顺利运行的前提是需要提前设定参数是需要求梯度的属性
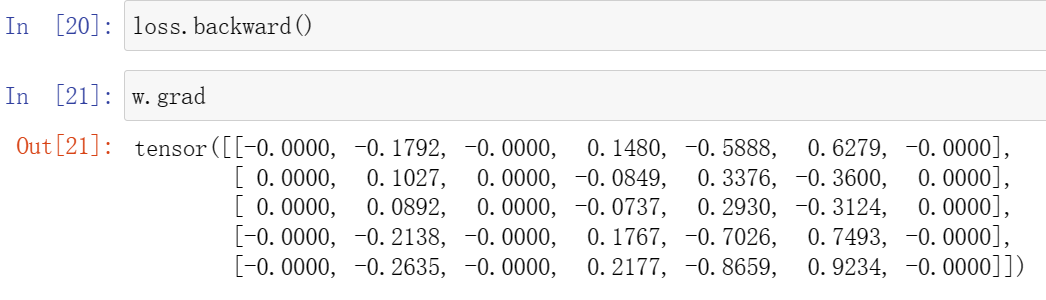
w.grad#查看w经过梯度下降所得的参数值,!还没有进行参数的更新!见(2)
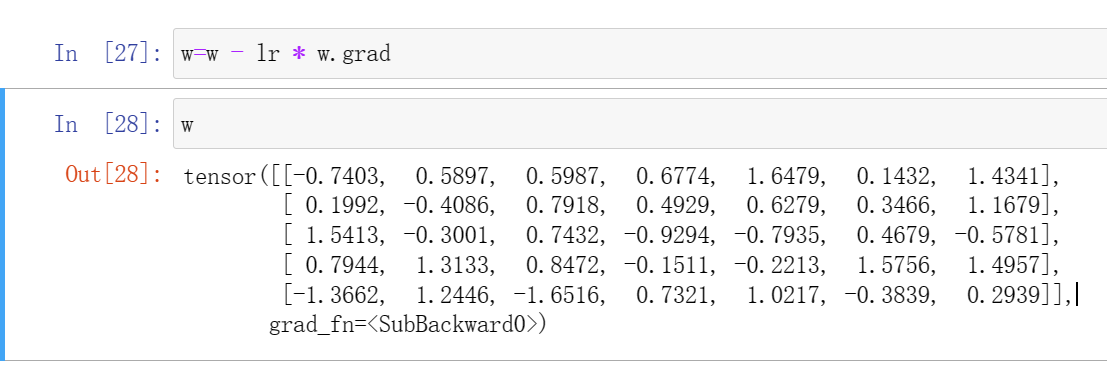
w=w -lr * w.grad#这步才是更新了参数(3)
|
两种损失函数
1.分类任务一般使用交叉熵损失函数:
$$
\text{Cross-Entropy}= -\sum_{i=1}^n [y_i \log(\hat{y}_i) + (1-y_i) \log(1-\hat{y}_i)]
\\y_i:\text{ 类别的真实标签(通常为0或1)}
\\\hat{y_i}: \text{对应类别的预测概率}
$$
2.回归任务一般使用均方误差损失函数
$$
\text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2
\\y_i:\text{真实值}
\\\hat{y_i}:预测值
\\n:样本数量
$$
损失函数使用时需注意该函数的传参
(1)结果:

(2)结果:
(3)结果:
搭建模型
搭建网络需要定义一个类,eg此处输入图像为rgb彩色图像,像素为48*48
ps: jupyter lab查看函数参数快捷键shift+tab
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class M_CNN(nn.Module):#定义网络,父类为之前导入的nn类
def __init__(self):#初始化
super().__init__()#父类的函数方法
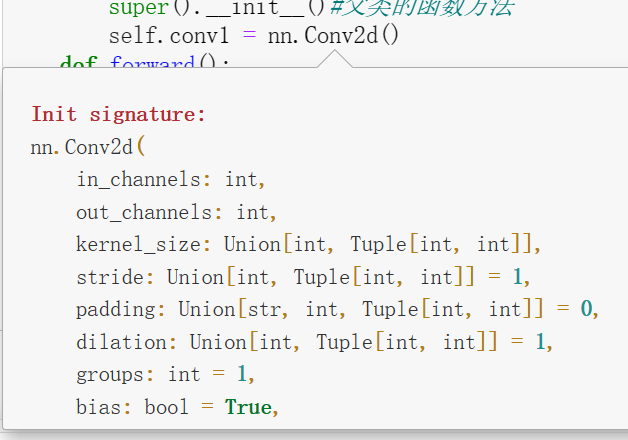
self.conv1 =nn.Conv2d(3,16,kernel_size=3,padding=1)#设计的卷积层,调用nn父类中的Conv2d卷积函数,参数见(4)eg:输入为彩色图像(输入为3),输出16个通道,卷积核大小为3*3;padding=1为填充1像素保证输出的长宽不变
self.conv2 =nn.Conv2d(16,32,kernel_size=3,padding=1)
self.bn1=nn.BatchNorm2d(16)#规范化,通道数为16#第一层卷积的输出通道数
self.bn2=nn.BatchNorm2d(32)
self.MaxPool=nn.MaxPool2d(kernel_size=2)#池化层
self.fc1=nn.Linear(12*12*32,1000)#网络全连接层,将处理完的输入图像所有像素拼接为一维,加入中间有1000个神经元的隐藏层
self.fc2=nn.Linear(1000,100)#1000个隐藏层1神经元,最送到100个隐藏层2神经元,由于12*12*32的输入太大,故需要不同神经元数目的隐藏层过渡
self.fc3=nn.Linear(100,7)#最后输出为7个神经元
def forward(self,x):
x=F.relu(self.bn1(self.conv1(x)))#输入先过卷积,后过规范器,最后通过激活函数relu,更新原有输入
x=self.MaxPool(x)#经过池化后图像宽高对半减
x=F.relu(self.bn2(self.conv2(x)))#经过第二个卷积层
x=self.MaxPool(x)
x=x.view(-1,12*12*32)#进入全连接之前,需要讲3维张量撑成1维的向量,-1代表可能用小批量进行训练,不确定数目,代表自适应,后面的数值代表进入的张量
x=F.relu(self.fc1(x))#进入全连接
x=F.relu(self.fc2(x))
x=F.relu(self.fc3(x))
return x
|
全连接层参数计算:
$$
一个(3,48\times48)图像通过一个(3,16,kernel=3\times3,步长为1)的卷积层,\\输出为(16,48\times48)图像,\\通过第一个池化层,窗口为2\times2,步长为2,\\输出为(16,24\times24),\\经过第二个卷积层(16,32,kernel=3\times3,步长为1)\\输出为(32,24\times24),\\通过第二个池化层,变为(32,12\times12)
$$
(4)nn.Conv2d函数的参数:
数据处理
读取数据,转化为dataset,再由dataset转化为dataloader
1
2
3
4
5
6
7
8
9
|
from torch.utils.data import DataLoader
from torchvision import datasets,tranforms
from torchvision.datasets import ImageFolder
transform=transforms.Compose([
transforms.ToTensor()#读取图像后将数据转换为tensor类型
transforms.Normalize(mean=(0.5,),std=(0.5,))#去均值,除标准差的归一化操作
])
dataset=ImageFolder('file_path',tansform=transform)#通过imagefolder来为读取的数据进行标注,后半部分使用tranform进行格式转化
dataloader=DataLoader(dataset,batch_size=32,shuffle=True)#shuffle意义为每个batch开始时顺序是否要被打乱
|
跑模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
#检测GPU使用情况
device=torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
print('Using device',device)
#创建模型
model=CNN_M().to(device)
#定义损失函数
loss_fun=F.cross_entropy
#定义优化器
opt=optim.Adam(model.parameters(),lr=0.01)#parameters为模型的所有参数
epochs=8#以batchsize为32的步长,每个批次通过一遍网络,直至所有样本被扫完作为一个epoch
for epoch in range(epochs):
for i,data in enumerate(dataloader,0):#每次的小batch做的事
inputs,labels=data[0].to(device),data[1].to(device)#input为作为输入的数据,labels为获取标签,to(device)为把数据往显卡里送
y=model(inputs)#进入模型的forward第一层到最后一层,结果给y
loss=F.cross_entropy(y,labels)#通过计算得的y与labels标签正确答案进行损失计算
loss.backward()#计算梯度值
opt.step()#优化器进行梯度下降,更新参数
opt.zero_grad()#参数的梯度清零,不然进入下一轮梯度计算时会累积上一次的结果
print(i,loss)
|
ps:最后来一张之前tutu带我看的不认识的Vtuber演唱会